如果信号中的某些频段混入了噪声，可以用低通滤波器、高通滤波器等对这些噪声进行过滤，但当信号中要是混入了白噪声这种没有明显频率段的噪声，这种滤波器的效果将会大大下降，这时就需要采用统计学的方法对信号进行估计，同时采用某种统计准则来衡量估计的误差，使得误差尽可能小，这种滤波器叫现代滤波器，其中简洁、高效的当属卡尔曼滤波。

《麻省理工学院技术评论》在一篇纪念卡尔曼先生的文章中提到道：“卡尔曼最重要的发明是卡尔曼滤波算法，该算法成就了过去50年间的许多基本技术，如把阿波罗号宇航员送上月球的航天计算机系统、把人类送去探索深海和星球的机器人载体，以及几乎所有需要从噪声数据去估算实际状态的项目。有人甚至把包括环绕地球的卫星系统、卫星地面站及各类计算机系统在内的整个GPS系统统称为一个巨大无比的卡尔曼滤波器。”

由此可见卡尔曼滤波在现代科学技术中的重要地位，而在SLAM中卡尔曼滤波也进行了广泛的应用，因此算法系列先讲一下卡尔曼滤波。

一、通俗解释

这个通俗解释是我在学习过程中偶然发现的文章，加上我的理解和解释，分享给大家。

假设一辆在公路上行驶的汽车，起点位置A，下一秒汽车驶入林荫道中的B点，再下一秒汽车驶出林荫道来到C点，行驶到B点的密林中因为我们眼睛看不到，真实位置是需要估计的。

这辆汽车上安装有IMU和GNSS（卫星）两种定位传感器。起点A的位置和速度假设是已知的，距离惯性坐标系X轴原点的距离为2m，速度为 $v_{t-1}$ 。

当车辆驶入到B点时，一方面我们可以根据IMU测量得到汽车本体的三轴加速度和三轴角速度，结合初始速度 $v_{t-1}$ ，便可以计算得到B点相对于A点在X轴方向行驶距离的估计值，这里我们假设估计值为10m（在SLAM系统中，这就是通过状态方程中代入里程计或者IMU测得的状态量估计值）

另一方面，通过GNSS我们可以直接测量出来B点的经纬度，通过坐标转换之后可以直接获得B点在X轴方向行驶的观测值，这里我们假设观测值为13m（在SLAM系统中，这就是通过观测方程代入激光雷达或相机数据测得的状态量估计值）

问题来了，距离惯性坐标系点的距离现在有估计值（12m=10m+2m）和观测值（13m）两个值，且两个值不一致，我们该如何确定B点的准确估计值呢？

众所周知，IMU测量汽车本体的加速度和角速度过程中，存在误差和噪声，GNSS通过卫星信号定位车辆经纬度的过程中也存在误差和噪声。

两种传感器给出的值都是一种概率最大，意思是在这个位置的概率最大，其它位置不是不可能只是概率较小。

而在卡尔曼滤波算法的理论中，无论是汽车上一秒的位置，IMU的测量数据，还是GNSS的直接观测值均被认为服从正态分布，服从正态分布的随机变量取与均值邻近的值的概率大，取与均值越远的值的概率越小，同时方差越小，分布越集中在均值附近，方差越大，分布越分散

这里我们假设A点位置Xt-1服从N(2,0.22)，如下图所示。从图中可以看出2m处纵坐标最大，概率最大，其它取值概率均小于此处。方差0.22则代表A点位置的误差水平。

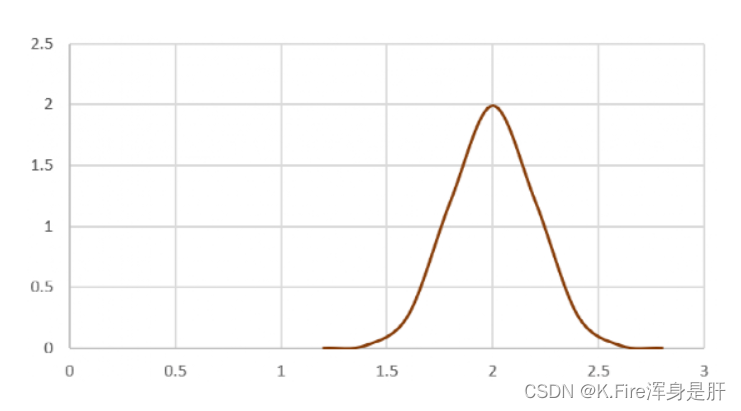
而对于IMU和GNSS这两种传感器来说，他们的噪声方差是可以测量的，在使用时是已知的，这里我们省略移动模型建模过程，直接假设基于IMU获得B点相对于A点的距离估计值XI服从N(10,0.12) ，方差0.12则代表IMU噪声的误差水平，此误差水平受IMU的精度，测量的累积时长有关。

GNSS通过卫星信号获得B点相对于原点的测量值XG服从N(13,0.42) ，方差0.42代表GNSS噪声的误差水平，此误差水平一方面受GNSS里卫星板卡的精度水平，另一方面主要受所处的环境有关，是否有遮挡，是否多金属环境等。由于B点处于林荫道下，卫星信号时有时无，因此此时0.42的误差水平还是比较高的。

现在我们有了两组数据，一组是B点相对于原点O的估计值XBOI = XI + XA = N(10,0.12) + N(2,0.22) = N(12,0.12 +0.22)，一组是B点相对于原点O的观测值XG = N(13,0.42)。

全文的高潮点来了，我该如何从两个概率分布中找到最准确的那个估计值呢，可以想象的是这个准确的估计值也遵从正态分布，这个正态分布的均值就是我们苦苦追寻的值。

卡尔曼给出的答案是，直接将两个概率分布相乘，即N(12,0.12 +0.22) * N(13,0.42)。

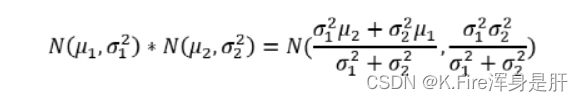
正态分布的乘法公式如上，将N(12,0.12 +0.22) * N(13,0.42)中的值带入下面公式，则可以得到如下正态分布。

B点的（12.23,0.192）又将作为计算C点位置的初始值，重复上述过程。

二、数学推导

1.问题建模

在很多实际问题中（如SLAM中估计机器人位姿），估计量不能通过直接测量得到，一般会用状态方程和观测方程来描述问题。

$x_{k}=g(x_{k-1},u_{k})+\varepsilon_{k}$

$z_{k}=h(x_{k})+\delta_{k}$

状态方程描述的是上一个状态 $x_{k-1}$ 在一定输入 $u_{k}$ （风力）的作用下到达当前时刻系统状态 $x_{k}$ 的过程，当然这个过程肯定存在一定噪声 $\varepsilon_{k}$ （轮胎打滑）

观测方程描述在当前时刻系统状态 $x_{k}$ 下观测 $z_{k}$ （GPS观测）的过程，也存在一定噪声 $\delta_{k}$ （GPS信号干扰）

这两个过程中的噪声都服从正态分布，假设 $\varepsilon_{k} \sim N(0,Q_{k}),\delta_{k} \sim N(0,R_{k})$

卡尔曼两遍只能处理线性系统，而这里的状态转移函数g和观测函数h往往是非线性函数，需要对其先进性线性化处理，一般线性化的方式都是泰勒展开，这个地方不具体讨论，展开后形式如下：

$x_{k}=A_{k}x_{k-1}+B_{k}u_{k}+\varepsilon _{k}$

$z_{k}=C_{k}x_{k}+\delta _{k}$

2.推导过程

（1）数学准备

首先引入一些数学上的概念。

协方差： $cov(X,Y)=E[(X-E[X]])(Y-E[Y])]=\frac{\sum_{i=1}^{N}(x_{i}-\overline{X})(y_{i}-\overline{Y})}{N-1}$

当状态量为m维向量时， $X=[X_{1},X_{2},...,X_{m}]^{T}$ ，这m个随机变量的协方差构成一个协方差矩阵P

另外，我们经常用MSE（均方误差）来衡量估计的准确性，MSE由方差加一个偏差项构成，在无偏估计下MSE就等于方差，也就是可以用方差去描述准确性，这时协方差矩阵的迹tr(P)也等于MSE。

另外还有一些矩阵求导的公式： $\frac{d}{dA}[tr(AB)]=B^{T};\frac{d}{dA}[tr(ABA^{T})]=2AB$

（2）具体推导

现在我们有了状态方程，已知上一个时刻状态和输入，以及系数，可以求出一个当前时刻状态的预测值（带噪声）；有了观测方程，已知观测 $z_{k}$ ，可以反求出一个当前时刻状态的预测值（带噪声），观测偏差可以表示为 $\widetilde{z_{k}}=z_{k}-{\widehat{z_{k}}}'=z_{k}-C_{k}{\widehat{x_{k}}}'$