神经网络和深度学习的简史_深度学习的故事

神经网络和深度学习的简史

神经网络如何从最早的人工智能时代发展到现在的故事。

神经网络和深度学习的简史

序幕——深度学习海啸

"深度学习的浪潮拍打着计算语言学的海岸已经好几年了，但2015年似乎是海啸的全部力量冲击主要的自然语言处理（NLP）会议的一年。" -克里斯托弗-D-曼宁博士，2015年12月

这听起来很夸张--说整个研究领域的既定方法很快就被一个新的发现所取代，就像被一场研究 "海啸 "击中一样。但是，这种灾难性的语言适合用来描述深度学习在过去几年中的流星式崛起--这种崛起的特点是对人工智能中最难解决的问题的统治性方法的大幅改进，来自谷歌等行业巨头的大量投资，以及研究出版物（和机器学习研究生）的指数式增长。

我上过几堂关于机器学习的课，甚至在本科生研究中使用过它，我不禁想知道这个新的 "深度学习 "是什么花哨的东西，还是只是80年代末已经开发的 "人工神经网络 "的放大版。让我告诉你，答案是一个相当精彩的故事--这个故事不仅仅是关于神经网络，不仅仅是关于一连串的研究突破，这些突破使深度学习在某种程度上比'大神经网络'更有趣（我将试图以一种几乎任何人都能理解的方式来解释），最重要的是几个不屈不挠的研究人员如何通过黑暗的几十年的放逐，最终赎回神经网络，实现深度学习的梦想。

序幕深度学习海啸

第一部分：开端（20世纪50年代至80年代）

几百年前的机器学习算法

虚假承诺的愚蠢之处

人工智能冬天的解冻

第二部分：神经网络绽放（20世纪80年代-2000年代）

神经网络获得视野

神经网络进入无监督状态

神经网络获得信仰

神经网络做出决定

神经网路变得更古怪

神经网络开始说话

一个新的冬天来临了

第三部分：深度学习（2000-2010年代）

对更多层次的资助

大数据的发展

蛮力的重要性

深度学习的方程式

尾声 深度学习的十年

第一部分：开端（20世纪50年代-80年代）

这是一个跨越半个世纪的故事的开始，关于我们如何学会让计算机学习。在这一部分中，我们将介绍神经网络在1958年以Perceptron诞生，70年代的人工智能寒冬，以及神经网络在1986年以反向传播重新流行。

几个世纪以来的机器学习算法

线性回归

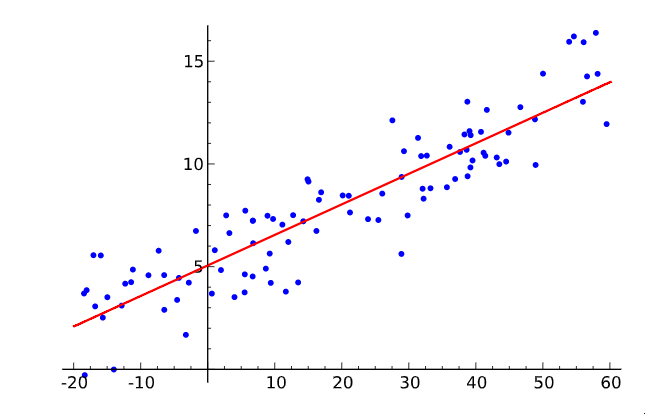
线性回归

让我们先简单介绍一下什么是机器学习。在一个二维图形上取一些点，然后画一条尽可能适合它们的线。你刚才所做的是将输入值（x）和输出值（y）的几对例子概括为一个可以将任何输入值映射到输出值的一般函数。

这就是所谓的线性回归，它是一种奇妙的、有200年历史的小技术，用于从一些输入-输出对中推断出一个一般的函数。这就是为什么拥有这样一种技术是美妙的：有大量的函数难以直接开发方程，但在现实世界中却很容易收集到输入和输出对的例子--例如，将一个口语的录音输入映射到该口语的输出的函数。

线性回归技术对于解决语音识别问题来说有点太弱了，但它所做的基本上就是监督式机器学习的全部内容。在给定的训练实例集上 "学习 "一个函数，每个实例都是该函数的一对输入和输出（我们将在稍后触及无监督的味道）。

特别是，机器学习方法应该推导出一个能够很好地概括不在训练集中的输入的函数，因为这样我们就可以实际地将其应用于我们没有输出的输入。例如，谷歌目前的语音识别技术是由机器学习提供的，它有一个庞大的训练集，但训练集还不如你可能要求你的手机理解的所有可能的语音输入那么大。

这个泛化原则非常重要，几乎总是有一个不属于训练集的测试数据集（更多的输入和输出的例子）。这个独立的数据集可以用来评估机器学习技术的有效性，看该方法在给定输入的情况下，有多少例子能正确计算出输出。

泛化的克星是过度拟合--学习一个对训练集非常有效的函数，但在测试集上却很糟糕。由于机器学习研究人员需要比较其方法的有效性，随着时间的推移，出现了训练集和测试集的标准数据集，可用于评估机器学习算法。

好了好了，定义够了。重点是--我们的画线练习是一个非常简单的有监督的机器学习的例子：点是训练集（X是输入，Y是输出），线是近似函数，我们可以用线来为不符合我们开始的任何点的X值找到Y值。别担心，这段历史的其余部分不会像这些那样干巴巴的。我们来了。

虚假承诺的愚蠢之处

既然这里的主题表面上是神经网络，为什么还要用线性回归来做这个序言？嗯，事实上，线性回归与第一个专门作为机器学习方法而设想的想法有一些相似之处。Frank Rosenblatt的Perceptron。

感知器

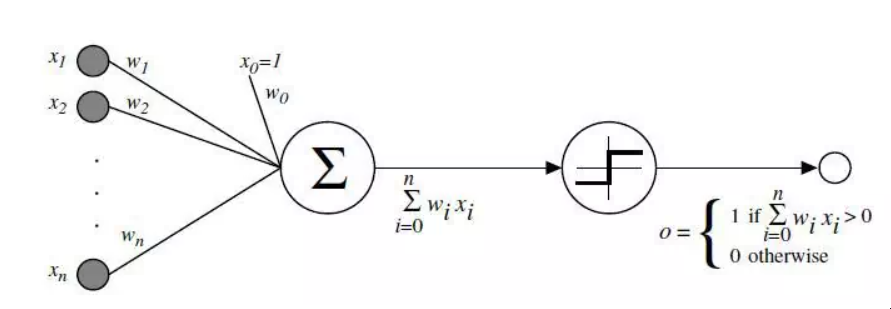
显示Perceptron如何工作的图表

作为一名心理学家，罗森布拉特将Percetron设想为我们大脑中的神经元如何运作的简化数学模型：它接受一组二进制输入（附近的神经元），将每个输入乘以一个连续值的权重（与附近每个神经元的突触强度），并对这些加权输入的总和进行阈值处理，如果总和足够大，就输出1，否则就输出0（与神经元发射或不发射的方式一样）。

一个感知器的大部分输入要么是一些数据，要么是另一个感知器的输出，但一个额外的细节是感知器也有一个特殊的 "偏置 "输入，它的值是1，基本上可以确保在相同的输入下有更多的函数可以计算，因为它能够抵消加起来的值。

这种神经元模型建立在沃伦-麦库洛赫和沃尔特-皮茨-麦库洛赫-皮茨的工作之上，他们表明，一个对二进制输入进行求和的神经元模型，如果求和超过一定的阈值，就输出1，否则就输出0，可以模拟基本的OR/AND/NOT函数。在人工智能的早期，这是件大事--当时的主流思想是，让计算机能够进行正式的逻辑推理，基本上就能解决人工智能。

感受器2

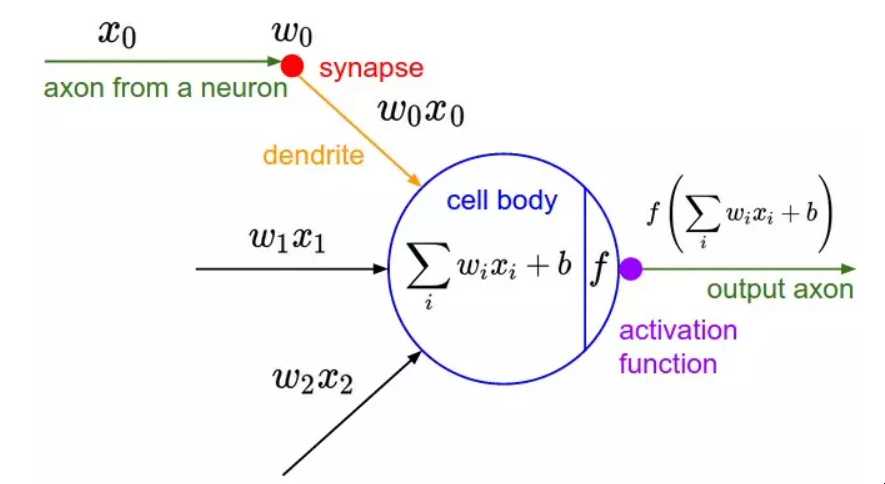
另一张图，显示了生物的灵感。激活函数就是人们现在所说的应用于加权输入和的非线性函数，以产生人工神经元的输出--在罗森布拉特的感知器中，该函数只是一个阈值操作。(资料来源)

然而，Mcculoch-Pitts模型缺乏一种学习机制，而这对于它能用于人工智能是至关重要的。这正是感知器的优势所在--罗森布拉特受唐纳德-赫伯的基础性工作启发，想出了一个让这种人工神经元学习的方法。赫伯提出了一个出人意料且影响巨大的观点，即知识和学习在大脑中主要是通过神经元之间突触的形成和变化发生的--简而言之就是赫伯规则。

"当细胞A的轴突足够接近激发细胞B，并反复或持续地参与激发它时，在一个或两个细胞中就会发生一些生长过程或代谢变化，从而使A作为激发B的细胞之一的效率得到提高。"

感知器并没有完全遵循这个想法，但是在输入端设置权重允许一个非常简单和直观的学习方案：给定一个输入-输出例子的训练集，感知器应该从中 "学习 "一个函数，对于每个例子，如果感知器对该例子的输入输出与该例子相比太低，则增加权重，否则，如果输出太高则减少权重。更加正式的说法是，该算法如下。

从具有随机权重和训练集的Perceptron开始 对于训练集中的一个例子的输入，计算感知器的输出。 如果Perceptron的输出与已知的对该例子正确的输出不一致。 如果输出应该是0但却是1，减少输入为1的权重。 如果输出应该是1但却是0，增加输入为1的权重。

转到训练集的下一个例子，重复步骤2-4，直到感知器不再犯错。 这个过程很简单，产生的结果也很简单：一个输入线性函数（加权和），就像线性回归一样，被一个非线性激活函数（和的阈值）"压扁"。当函数只能有一组有限的输出值时，对总和进行阈值处理是很好的（如逻辑函数，在这种情况下只有两个--真/1和假/0），因此，问题不在于为任何一组输入产生一个连续编号的输出--回归--而是用一个正确的标签对输入进行分类--分类。

康奈尔航空实验室的Mark I Perceptron"，第一个Perceptron的硬件实现（来源：维基百科/康奈尔图书馆）

罗森布拉特在定制的硬件中实现了感知器的想法（这时花哨的编程语言还没有普遍使用），并表明它可以用来学习对20x20像素的输入进行正确的简单形状分类。就这样，机器学习诞生了--一台计算机被建造出来，它可以根据已知的输入和输出对近似地计算出一个函数。在这种情况下，它学会了一个小玩具函数，但不难设想出有用的应用，如将混乱的人类手写体转换为机器可读的文本。

但是等等，到目前为止，我们只看到了一个感知器是如何学习输出1或0的--这怎么能扩展到对有许多类别的分类任务，比如人类笔迹（其中有许多字母和数字作为类别）的工作？这对一个感知器来说是不可能的，因为它只有一个输出，但是有多个输出的函数可以通过在一个层中有多个感知器来学习，这样所有这些感知器都收到相同的输入，每个感知器负责函数的一个输出。

事实上，神经网络（或正式称为 "人工神经网络"--ANN）只不过是一层层的Perceptrons--或神经元，或单元，正如它们今天通常所称--在这个阶段，只有一层--输出层。因此，神经网络使用的一个原型例子是对手写数字的图像进行分类。输入是图像的像素，有10个输出神经元，每个神经元对应10个可能的数字值中的一个。在这种情况下，10个神经元中只有一个输出1，最高的加权和被认为是正确的输出，其余的都输出0。

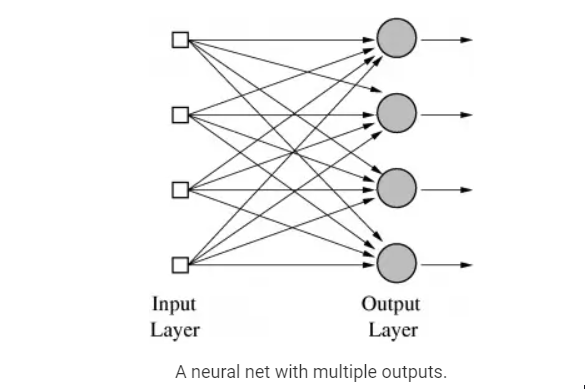
带有输出层的神经网。

一个有多个输出的神经网。

也有可能设想出与Perceptron不同的人工神经元的神经网。例如，阈值激活函数不是严格必要的；Bernard Widrow和Tedd Hoff很快在1960年用 "一个使用化学 "记忆体 "的自适应 "ADALINE "神经元 "探索了只输出权重输入的选项，并展示了这些 "自适应线性神经元 "是如何被纳入带有 "记忆体 "的电路中的--有记忆的电阻。

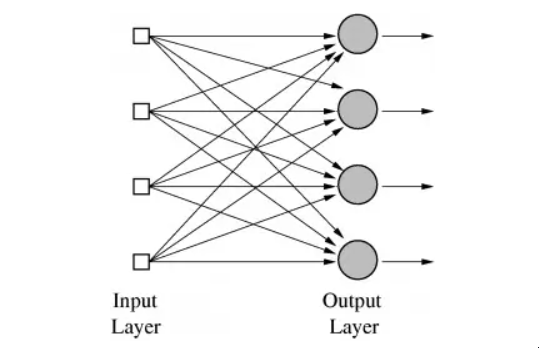
他们还表明，没有阈值激活函数在数学上是很好的，因为神经元的学习机制可以通过良好的微积分在形式上基于最小化误差。你看，由于神经元的功能没有因为从0到1的急剧阈值跳跃而变得奇怪，当每个权重改变时，对误差变化程度的测量（导数）可以用来降低误差并找到最佳权重值。正如我们将看到的，使用训练误差与每个权重的导数来寻找正确的权重，正是至今为止神经网络的典型训练方式。

如果我们对ADALINE多做一些思考，我们会有进一步的认识：为一些输入寻找一组权重实际上只是一种线性回归的形式。而且，和线性回归一样，这也不足以解决语音识别或计算机视觉的复杂人工智能问题。麦卡洛、皮茨和罗森布拉特真正兴奋的是连接主义的广泛理念：由这种简单的计算单元组成的网络可以强大得多，可以解决人工智能的困难问题。而且，罗森布拉特也是这么说的，就像当时《纽约时报》上这段坦率可笑的引文一样。

"海军今天揭示了一种电子计算机的胚胎，它期望能够走路、说话、看东西、写字、自我复制和意识到自己的存在......水牛城康奈尔航空实验室的研究心理学家弗兰克-罗森布拉特博士说，Perceptrons可能会作为机械太空探险家被发射到行星上"

或者，看一下当时的这个电视片断。

这段视频中承诺的东西--仍然没有真正出现。

这种谈话无疑激怒了人工智能的其他研究人员，他们中的许多人正专注于基于操纵符号的方法，这些符号有具体的规则，遵循逻辑的数学规律。麻省理工学院人工智能实验室的创始人马文-明斯基（Marvin Minsky）和当时的实验室主任西摩-帕珀特（Seymour Papert）是一些对炒作持怀疑态度的研究人员，他们在1969年以严格分析Perceptrons的局限性的形式在一本名为Perceptrons的开创性著作中发表了他们的怀疑态度。

有趣的是，Minksy实际上可能是第一个用1951年的SNARC（随机神经模拟强化计算器）实现硬件神经网的研究者，这比Rosenblatt的工作早了很多年。但是，他在这个系统上的工作没有任何痕迹，而《感知器》中的分析的关键性质表明，他认为这种人工智能的方法是一个死胡同。

这个分析中最广泛讨论的内容是阐明了感知器的局限性--例如，它们不能学习简单的布尔函数XOR，因为它不是线性可分离的。虽然这里的历史很模糊，但人们普遍认为这篇论文帮助迎来了第一个人工智能寒冬--在人工智能的大规模炒作浪潮之后的一个时期，其特点是幻想破灭，导致资金和出版物冻结。

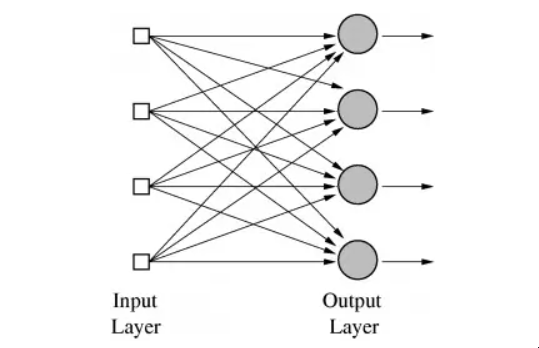
感知器的局限性的可视化。在输入X,Y上找到一个线性函数来正确输出 "+"或"-"，相当于在这个二维图上画一条线，把所有 "+"的情况和"-"的情况分开；显然，对于第三种情况，这是不可能的。

人工智能冬天的解冻 所以，对于神经网络来说，事情并不乐观。但为什么呢？毕竟，我们的想法是结合一堆简单的数学神经元来做复杂的事情，而不是使用单一的神经元。换句话说，不是只有一个输出层，而是向任意多的神经元发送输入，这些神经元被称为隐藏层，因为它们的输出作为另一个隐藏层或输出层神经元的输入。只有输出层的输出被 "看到"--它是神经网的答案--但所有由隐藏层完成的中间计算可以解决比单层复杂得多的问题。

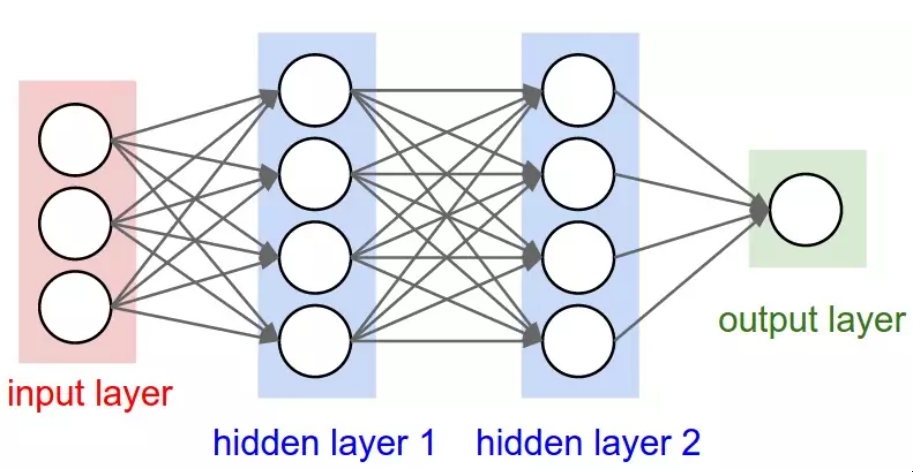
隐蔽层 有两个隐藏层的神经网（优秀来源）

隐藏层之所以好，从根本上说，是隐藏层可以在数据中找到特征，并允许下面的层在这些特征上操作，而不是在嘈杂和庞大的原始数据上。例如，在非常常见的在图像中寻找人脸的神经网络任务中，第一个隐藏层可以接收原始像素值，并在图像中找到线、圆、椭圆等。下一层将接收这些线、圆、椭圆等在图像中的位置，并利用这些来寻找人脸的位置--这就更容易了！

人们基本上都明白这一点。而人们，基本上都明白这一点。事实上，直到最近，机器学习技术通常不直接应用于原始数据输入，如图像或音频。相反，机器学习是在数据经过特征提取后进行的--也就是说，为了使学习更容易，机器学习是在预处理的数据上进行的，从这些数据中已经提取了更多有用的特征，如角度或形状。

特征提取

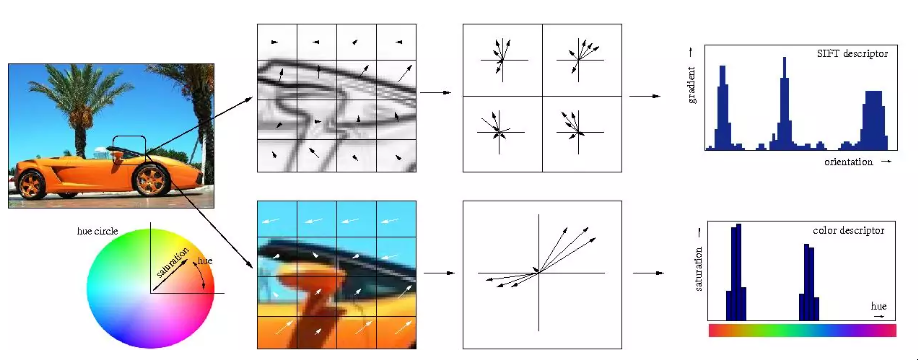
传统手工特征提取的可视化

因此，需要注意的是，Minsky和Papert对Perceptrons的分析并不只是表明用单个Perceptron计算XOR是不可能的，而是特别认为必须用多层Perceptrons--也就是我们现在所说的多层神经网络--来完成，而Rosenblatt的学习算法对多层是不起作用的。这就是真正的问题所在：之前为Perceptron概述的简单学习规则对多层不起作用。为了了解原因，让我们重申一下单层感知器是如何学习计算一些函数的。

等于函数输出数量的Perceptrons的数量将以小的初始权重开始。

对于训练集中一个例子的输入，计算Perceptrons的输出

对于每个感知器，如果输出与例子的输出不一致，相应地调整权重

转到训练集中的下一个例子，重复步骤2-4，直到感知器不再犯错。

这样做对多层不起作用的原因应该是很直观的：例子只指定了最后输出层的正确输出，那么我们到底应该如何知道如何调整之前各层的Perceptrons的权重？答案，尽管需要一些时间来推导，但事实证明，它再次基于古老的微积分：连锁规则。

关键的认识是，如果神经网的神经元不完全是Perceptrons，而是用一个激活函数来计算输出，这个激活函数仍然是非线性的，但也是可微的，就像Adaline那样，不仅可以用导数来调整权重，使误差最小化，而且链规也可以用来计算前一层所有神经元的导数，从而也可以知道调整其权重的方法。

或者，更简单地说：我们可以用微积分将输出层中任何训练集错误的部分责任分配给前一个隐藏层中的每个神经元，然后我们可以进一步分担责任，如果还有另一个隐藏层，以此类推--我们反向传播错误。就这样，我们可以发现，如果我们改变神经网中的任何权重，包括隐藏层中的权重，误差会有多大的变化，并使用优化技术（很长一段时间，通常是随机梯度下降）来寻找最佳权重，使误差最小。

逆向传播

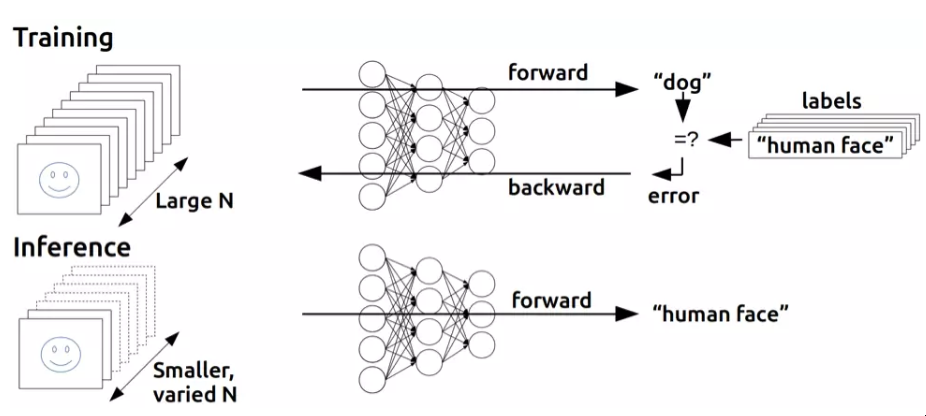
反向传播的基本思想。(来源)

Backpropagation是由多个研究人员在60年代早期得出的，并且早在1970年就由Seppo Linnainmaa实现了在计算机上的运行，但Paul Werbos在1974年的博士论文中深入分析后，在美国首先提出它可以用于神经网络。有趣的是，就像感知器一样，他的灵感松散地来自于对人类思维的建模工作，在这种情况下，正如他自己所叙述的，是弗洛伊德的心理学理论。

"1968年，我提议我们以某种方式模仿弗洛伊德的概念，即信用分配的逆向流动，从神经元流回神经元......我用直觉和例子以及普通的连锁规则的组合来解释逆向计算，尽管这也正是弗洛伊德以前在其心理动力学理论中提出的东西在数学中的转化！"

尽管解决了多层神经网如何训练的问题，并在撰写博士论文时看到了这个问题，但由于人工智能寒冬的影响，韦尔博斯直到1982年才发表了关于Backprop在神经网中的应用。事实上，Werbos认为这种方法对于解决Perceptrons中指出的问题是有意义的，但整个社区对解决这些问题失去了信心。

"明斯基的书最有名的是认为（1）我们需要使用MLP[多层感知器，多层神经网络的另一个术语]，即使是代表简单的非线性函数，如XOR映射；（2）地球上没有人找到一个可行的方法来训练MLP，足以学习这样的简单函数。明斯基的书使世界上大多数人相信，神经网络是一个没有信誉的死胡同--最糟糕的一种异端。

Widrow强调，这种悲观主义压制了早期的 "感知器 "人工智能学派，不应该真正归咎于明斯基。明斯基只是总结了数百名真诚的研究人员的经验，他们试图找到训练MLP的好方法，但无济于事。曾经有一些希望之岛，比如罗森布拉特称之为 "反向传播 "的算法（与我们现在所说的反向传播完全不同！），以及阿玛里的简短建议，即我们可以考虑将最小二乘法[简单线性回归的基础]作为训练神经网络的一种方法（没有讨论如何获得导数，并警告说他对这种方法不抱太大期望）。

但当时的悲观情绪变成了终结。1970年代初，我确实在麻省理工学院拜访了明斯基。我提议我们做一篇联合论文，说明MLP事实上可以克服早期的问题......但明斯基不感兴趣(14)。事实上，在麻省理工学院或哈佛大学或我能找到的任何地方，当时都没有人感兴趣"。

似乎正是由于这种学术兴趣的缺乏，直到十多年后的1986年，这种方法才在David Rumelhart、Geoffrey Hinton和Ronald Williams的《通过反向传播错误学习表征》中得到推广。尽管有很多人发现了这一方法（该论文甚至明确提到David Parker和Yann LeCun是事先发现这一方法的两个人），但1986年的出版物因其对这一想法的简明扼要的阐述而脱颖而出。事实上，作为一个机器学习的学生，很容易发现他们论文中的描述与教科书和人工智能课程中解释这一概念的方式基本相同。IEEE上的一篇回顾文章也呼应了这一概念。

"不幸的是，Werbos的工作在科学界几乎无人知晓。1982年，帕克重新发现了这项技术[39]，并于1985年在M.I.T.发表了一份关于这项技术的报告[40]。在帕克发表他的发现后不久，鲁梅尔哈特、辛顿和威廉姆斯[41]、[42]也重新发现了这项技术，而且主要是由于他们在其中提出了清晰的框架，他们最终成功地使这项技术广为人知"。

但这三位作者不仅仅是提出了这种新的学习算法，还走得更远。同年，他们发表了更深入的《通过误差传播学习内部表征》，专门解决明斯基在《感知器》中讨论的问题。虽然这个想法是由过去的人设想出来的，但正是1986年的这个表述，使人们广泛了解到多层神经网络如何被训练来解决复杂的学习问题。就这样，神经网络又回来了! 接下来，我们将看到仅仅几年后，反向传播和 "通过误差传播学习内部表征 "中讨论的其他一些技巧是如何被应用到一个非常重要的问题上的：使计算机能够阅读人类的手稿。

第二部分：神经网络开花结果（20世纪80年代-2000年代）

神经网络获得视觉 LeNet Yann LeCun演示的LeNet（来源）

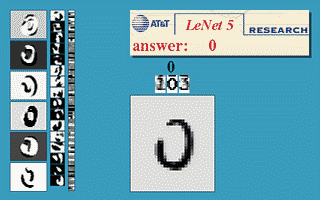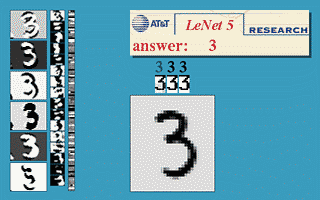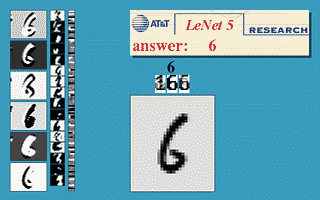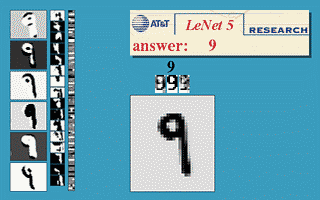
随着训练多层神经网络的秘密被揭开，这个话题再次变得炙手可热，Rosenblatt的崇高野心似乎也可以实现了。直到1989年，另一个关键的发现才被发表，现在已经被教科书和讲座所普遍引用。"多层前馈网络是通用的近似器"。从本质上讲，它从数学上证明了多层神经网络在理论上可以实现任何功能，当然还有XOR。

但是，这是数学，你可以想象有无尽的内存和计算能力，如果需要的话--反向传播允许神经网络在现实世界中用于任何东西吗？

哦，是的。同样在1989年，AT&T贝尔实验室的Yann LeCun等人在 "Backpropagation Applied to Handwritten Zip Code Recognition "中展示了Backpropagation的一个非常重要的现实世界应用。

你可能认为计算机能够正确地理解手写数字是相当不令人印象深刻的，而且现在它确实是相当古怪的，但是在该出版物发表之前，我们人类的混乱和不一致的涂鸦证明了对计算机的更整洁的头脑的重大挑战。该出版物使用了美国邮政局的一个大型数据集，表明神经网络完全有能力完成这项任务。更重要的是，它首次强调了对神经网络进行关键修改的实际需要，超越了普通的反向传播，走向现代深度学习。

"视觉模式识别的经典工作已经证明了提取局部特征并将其结合起来形成高阶特征的优势。通过强迫隐藏单元只结合局部信息源，这种知识可以很容易地建立在网络中。一个物体的独特特征可能出现在输入图像的不同位置。

因此，有一组特征检测器可以在输入位置的任何地方检测到一个特定的特征实例，这似乎是明智的。由于特征的精确位置与分类无关，我们可以承受在这个过程中损失一些位置信息。尽管如此，必须保留近似的位置信息，以允许下一级检测更高阶、更复杂的特征（Fukushima 1980；Mozer 1987）"。

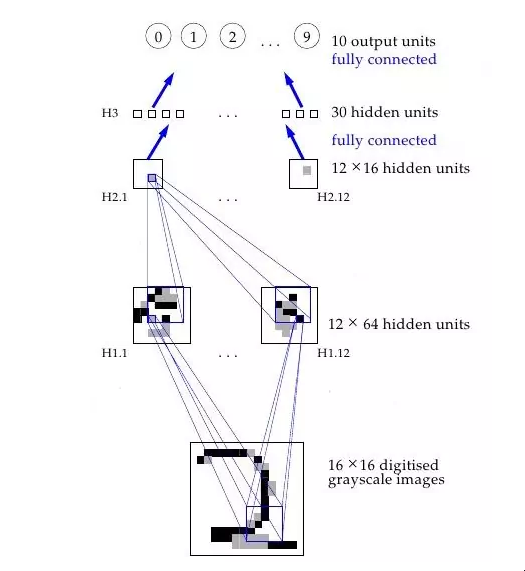
CNN

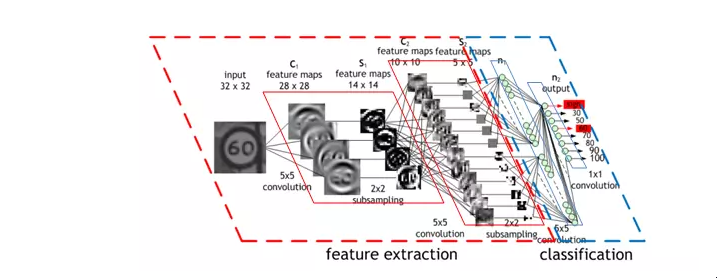这个神经网的工作原理的可视化。(资料来源)

或者，更具体地说：神经网络的第一个隐藏层是卷积的--而不是每个神经元对输入图像的每个像素都有不同的权重（40x60=2400个权重），神经元只有一小套权重（5x5=25），这些权重被应用于相同大小的图像的一大堆小子集。因此，举例来说，与其让4个不同的神经元学习检测输入图像的4个角的45度线，

不如让一个神经元学习检测图像子集的45度线，并在其中各处进行检测。第一层之后的各层也以类似的方式工作，但吸收了前一个隐藏层中发现的 "局部 "特征，而不是像素图像，因此 "看到 "图像的更大部分，因为它们结合了图像中越来越大的子集信息。最后，最后两层是普通的神经网层，使用卷积层产生的高阶大特征来确定输入图像对应的数字。这篇1989年的论文中提出的方法后来成为国家部署的支票阅读系统的基础，正如LeCun在这段视频中所展示的。

这一点之所以有帮助，即使在数学上不是很清楚，也是很直观的：如果没有这样的约束，网络将不得不为图像的每一部分学习同样简单的东西（如检测45度线、小圆圈等）一大堆时间。但有了这个约束，只有一个神经元需要学习每个简单的特征--而且总体上权重要少得多，它可以做得更快 此外，由于这种特征的像素精确位置并不重要，神经元在应用权重时基本上可以跳过图像的相邻子集--子采样，现在被称为池化的一种类型--从而进一步减少训练时间。增加这两种类型的层--卷积层和池化层--是卷积神经网络（CNNs/ConvNets）与普通神经网络的主要区别。

CNN 2 一个漂亮的CNN操作的可视化图（来源）

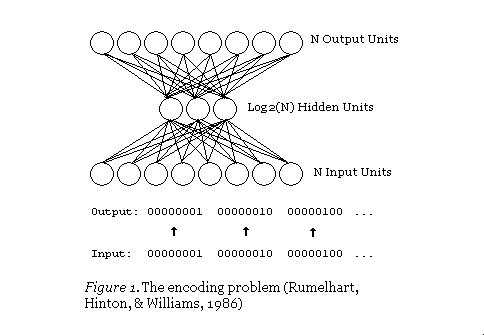
当时，卷积思想被称为 "权重共享"，实际上在1986年Rumelhart、Hinton和Williams对反向传播的扩展分析中已经讨论过。实际上，功劳甚至可以追溯到更早--Minsky和Papert在1969年对Perceptrons的分析足够透彻，提出了一个激发这个想法的问题。但是，和以前一样，其他人也独立探索了这个概念--即福岛邦彦在1980年提出的神经认知器的概念。而且，和以前一样，它背后的想法从对大脑的研究中获得了灵感。

"根据Hubel和Wiesel的层次模型，视觉皮层的神经网络有一个层次结构。LGB（外侧膝状体）->简单细胞->复杂细胞->低阶超复杂细胞->高阶超复杂细胞。还有人认为，低阶超复杂细胞和高阶超复杂细胞之间的神经网络具有类似于简单细胞和复杂细胞之间