线性回归算法_线性回归训练集测试集

作者：小丑西瓜9 | 2024-04-07 21:39:16

踩

线性回归训练集测试集

一维线性Y=wx+b ，回归就是预测输出值，调整w，b；输入是x，输出预测是y

MSE=[∑（y-yi）^2 ]/n m是均值，s是二次方，e是误差（要求MSE最小）

有解析解与无解析解：有解析解---->w,b是能够求解出来的；无解析解--->参数求解不出来，需要通过模型计算出来

输入输出的向量[]：代表着多输入多输出

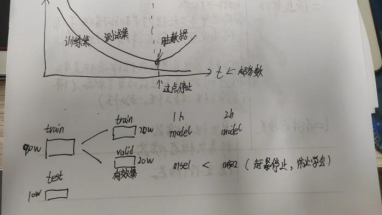
训练集（80%）--->训练出一个模型；测试集（20%）--->测试一个模型的准确度

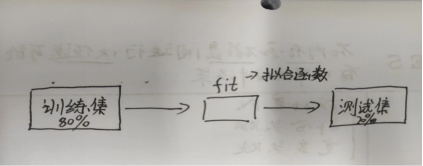
推广能力（泛化能力）：能在测试集上表现良好的能力

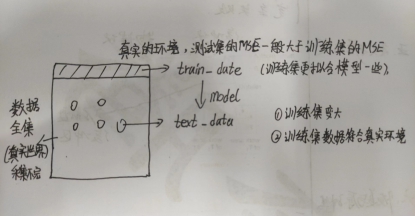
测试集MSE和训练集的MSE谁大谁小：

（1）理论上，测试集MSE比训练集的MSE大，也有可能比训练集MSE小

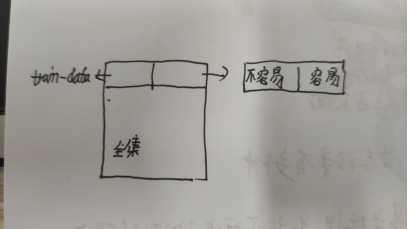
（2）但是真实环境中测试集很难采集到比训练集低的数据，所以工程上比训练集高的数据

（3）解决方法：增大训练集的数据量，增加训练集的多样性

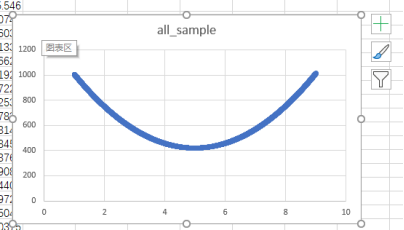
MSE=（y-yi）^2与绝对值=|y-yi|：一堆数据点，有些难预测，有些好预测

（1）MSE=（y-yi）^2，把容易预测的MSE降低到一定程度后，在优化容易点的MSE，收益上就会变小很多；然后就会把注意力调向难预测的点

（2）绝对值=|y-yi|，用绝对值误差，收益上永远不变，注意力一直会在容易点上面

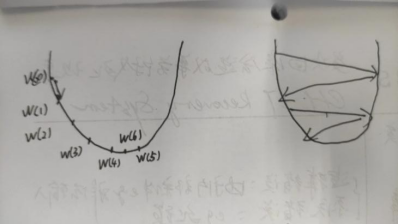
MSE=∑（wx+b-y）^2 /n，求最小值

dMSE/dw=∑（wx+b-y）2*x /n

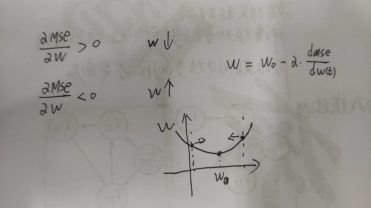
W（1）=w（0）- dMSE/dw（0）

W（2）=w（1）- dMSE/dw（1）

梯度下降法：

学习因子：α

W(t+1)=w(t)-α*dMSE/dw(t)

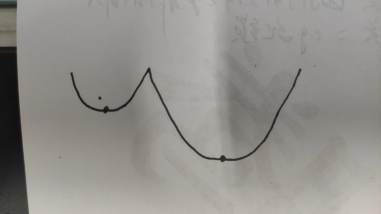
局部最小值：随机多采样多地方值

dMSE/dw=∑（wx+b-y）2*x /n=0，是否可以直接求解

存在解，因为n过大直接解方程未必能解得出w

所以要用梯度下降法求解w

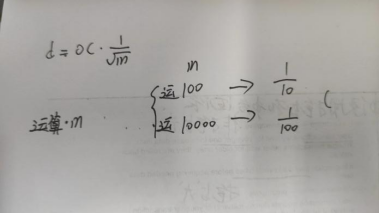
n太大时，需要取随机m来代替，取值近似2,4,8,16,32,64……

MSE并不是越来越小的好，很有可能过拟合，学习到脏数据，使得测试变得不准确

m测出来MSE的幅度d=oc* 1/ （m^1/2）成正比，m越大，MSE更加接近真实值

m越大，d带来的幅度越小，性价比不高

多元线性回归y=wx+w0（x=x1，……，xn； w=w1，……，wn）

使用线性回归的前提条件：数据尽量在一条直线上

二元线性回归y=w1*x^2+w2*x+w0：在训练集上要比一元线性回归带来的收益更好，w2能够等于0

多项多元线性回归y=w1*x+w2*x^2+……+wn*x^n+w0：任何函数都能够分解（n趋近于∞），容易过拟合训练集，把其中的噪声也给吸收进来，训练测试集误差就会很大；所以n（trade off）就需要适可而止，不光为了减低运算量，也可以防止过拟合

线性回归花式玩法：更好理解线性回归，w也不代表权值

(1)抗噪声：x1-->y变成[x1,x2]-->y(x1是正常数据，x2是随机产生的数据，与回归无关)

y=w1*x1+w2*x2+w0------>w2会趋向于0的

(2)防冗余：x-->y变成[x,x]-->y(把x拆分成两个变量x，x)

y=w1*x+w2*x+w0------->w1与w2相加之和等于w，且两者还相等


# -*- encoding:utf-8 -*-
from sklearn import datasets
from sklearn.model_selection import train_test_split 
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_predict
from numpy import shape
from sklearn import metrics
import numpy as np
def extend_feature(x):
    result=[x[0],x[0]]
    result.extend(x[1:])
    return result
    #return [x[0],x[0]]
def read_data(path):
    with open(path) as f :
        lines=f.readlines()
    lines=[eval(line.strip()) for line in lines]
    X,y=zip(*lines)
    X=[extend_feature(x) for x in X]
    X=np.array(X)
    y=np.array(y)
    return X,y
 
X_train,y_train=read_data("train_data")
X_test,y_test=read_data("test_data")
 
 #一个对象，它代表的线性回归模型，它的成员变量，就已经有了w，b
model = LinearRegression()
#一调用这个函数，就会不停的找合适的w和b，直到误差最小，拟合函数
model.fit(X_train, y_train)
 
print (model.coef_)#打印w
print (model.intercept_)#打印w0 就是b
 
y_pred = model.predict(X_train)
print ("MSE:", metrics.mean_squared_error(y_train, y_pred))
 
y_pred = model.predict(X_test)
print ("MSE:", metrics.mean_squared_error(y_test, y_pred))

本文内容由网友自发贡献，转载请注明出处：https://www.wpsshop.cn/w/小丑西瓜9/article/detail/380803?site

线性回归算法_线性回归 训练集 测试集

线性回归算法_线性回归训练集测试集