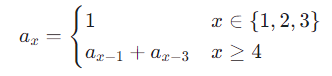矩阵及矩阵快速幂

知识点

矩阵简介

矩阵是一个由实数组成的长方形集合。
行数和列数相等的矩阵叫做方阵。
下面就是一个方阵。

矩阵加减法及矩阵数乘

两个矩阵相加就是两个矩阵对应位置相加
如矩阵$(1,-1,2)+(3,5,5)=(4,4,7)$
两个矩阵相减就是两个矩阵对应位置相减
如矩阵$(9,10,7)-(3,5,5)=(6,5,2)$
矩阵数乘就是用一个数乘一个矩阵，将矩阵里的每个数都乘上那个数就行了，
如矩阵$(9,5,7)\ast 3=(27,15,21)$

矩阵乘法

矩阵乘法就有点复杂了。
首先，一个n行k列的矩阵A乘上一个k行m列的矩阵B等于一个n行m列的矩阵C。
然后用A的第一行乘上B的第一列，依次对应好相乘再求和，作为C的第一行的第一个数，
用A的第一行乘上B的第二列，依次对应好相乘再求和，作为C的第一行的第二个数，以此类推
注意：矩阵乘法中$A\ast B!=B\ast A$
代码

Mat ans(r, t.c);  
     int n = r, m = t.c;
      for (int i = 1; i <= n; i++){
	for (int j = 1; j <= m; j++){
		for (int k = 1; k <= c; k++){
			ans.a[i][j] += a[i][k] * t.a[k][j];
		}
	}
}            
1
2
3
4
5
6
7
8
9

矩阵快速幂

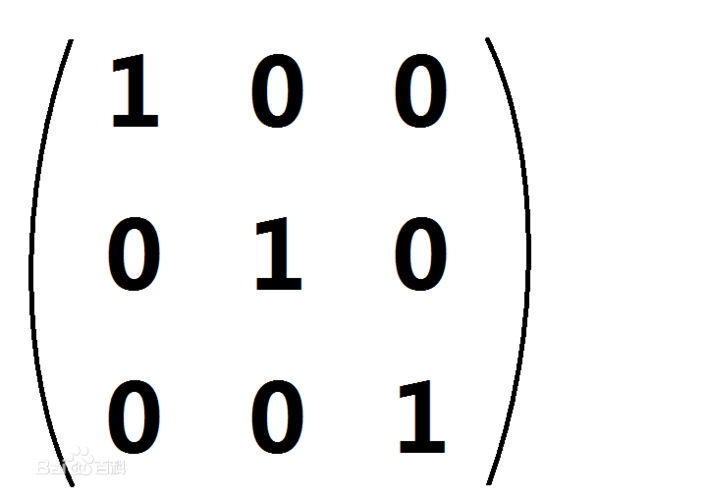
在矩阵乘法中有一种单位矩阵乘任何矩阵都不会变，也就是单位矩阵$\ast A=A$(A是任意矩阵)
他的左对角线上的数全是1，其余是0，如：

矩阵快速幂和整数快速幂相似，只不过是把整数的乘法变成了矩阵乘法。
代码

Mat ans(r,c);
ans.unit();
Mat a = *this;
while(b){
	if(b&1){
		ans=ans*a;
		ans=ans%p;
	}
	a=a*a;
	a=a%p;
	b>>=1;
}    
1
2
3
4
5
6
7
8
9
10
11
12

例题

矩阵加速

时间限制：1秒 内存限制：128M

题目描述

已知一个数列a，满足：

求a数列的第n项模$10^9+7$的值。

样例输入

3
6
8
10
1
2
3
4

样例输出

4
9
19
1
2
3

思路

可以用矩阵快速幂进行递推
设一个矩阵
$(a_x,$
$a_{x+1},$
$a_{x+2})$
再构造出一个矩阵
$(0,1,0$
$0,0,1$
$1,0,1)$
它俩相乘可得
$(a_{x+1}$
$a_{x+2}$
$a_{x+3})$
利用矩阵快速幂可解决此题

代码

#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
long long p=1e9+7;
const int N=105;
struct Mat {
    long long a[N][N];
    int r, c;
    Mat(int _r = 0, int _c = 0) {
        r = _r, c = _c;
        memset(a, 0, sizeof a);
        if (c == 0)
            c = r;  
    }
    Mat operator*(const Mat t) const {
        Mat ans(r, t.c);  
        int n = r, m = t.c;
        for (int i = 1; i <= n; i++){
			for (int j = 1; j <= m; j++){
				for (int k = 1; k <= c; k++){
					ans.a[i][j] += a[i][k] * t.a[k][j];
				}
			}
		}            
        return ans;
    }
    Mat operator%(const long long t) const {
        Mat ans=*this;
        for(int i=1;i<=r;i++){
        	for(int j=1;j<=c;j++){
        		ans.a[i][j]=ans.a[i][j]%t;
			}
		}
		return ans;
    }
    void unit() {
    	memset(a,0,sizeof a);
    	for(int i=1;i<=min(r,c);i++){
    		a[i][i]=1;
		}
	}
	Mat fast_pow(long long b,long long p) {
		Mat ans(r,c);
		ans.unit();
		Mat a = *this;
		while(b){
			if(b&1){
				ans=ans*a;
				ans=ans%p;
			}
			a=a*a;
			a=a%p;
			b>>=1;
		}
		return ans%p; 
	}
}ans(3,1),a(3,1),fac(3,3);
int main() {
	int t;
	scanf("%d",&t);
	while(t--){
		long long n;
		scanf("%lld",&n);
		if(n<=3){
			printf("1\n");
			return 0;
		}
		a.a[1][1]=1;
		a.a[2][1]=1;
		a.a[3][1]=1;
		fac.a[1][2]=1;
		fac.a[2][3]=1;
		fac.a[3][1]=1;
		fac.a[3][3]=1;
		Mat po=fac.fast_pow(n-1,p);
		ans=(po*a)%p;
		printf("%lld\n",ans.a[1][1]);
	}
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81