数据结构【线性表-链表】_单链表adt

线性表的链式存储结构：

为了表示数据元素ai和其后继元素ai+1之间的逻辑关系，对ai来说需存储其本身信息和后继元素的信息（存储位置）。这两部分组成ai的存储映像，称为结点（Node），它包含两个域：数据域和指针域。n个结点链结在一起，就组成线性表的链式存储结构。

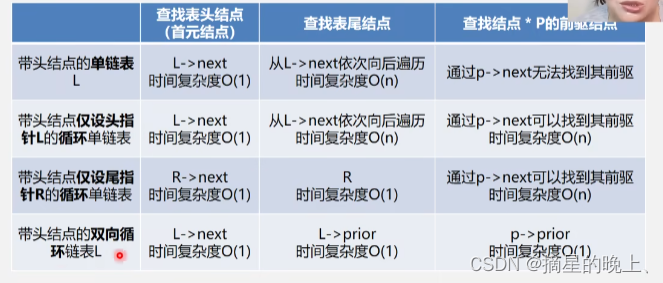
我们首先来看一下最简单也是最常用的单链表。前面我们已经了解到，链表中我们把每个内存块叫做链表的一个结点。为了将每个结点连接到一起，每个结点不仅存储数据，而且还需要记录下一个结点的地址。我们把这个记录下一个结点的指针称为后继指针next。单链表是单方向顺序的一个线性表。其中有两个结点比较特殊，分别是第一个和最后一个结点。我们通常把第一个结点叫做头结点，最后一个结点叫做尾结点，头结点用来记录链表的基地址，这样我们就可以遍历得到整个结点，尾结点是最后一个结点，它的指针指向一个空地址NULL，这样我们通过判断后继指针next是不是NULL来确定某个结点是不是尾结点。
1）单向链表

using namespace std;
struct Node
{
	int value;
	Node *next;
}*LinkedList,LNode;
1
2
3
4
5
6

接下来我们来看下双向链表，单链表只有一个指针，每个结点都只有一个后继指针next指向下一个结点的地址。而双向链表，顾名思义，它有两个方向，所以每个结点不仅有一个指向下一个结点的后继指针next，还有一个指向前一个结点的前驱结点prev。与单链表相比，双向链表的每个结点还需要存储指向前一个结点的指针，所以，同样多的数据，双向链表比单链表需要更多的存储空间。两个指针虽然比较浪费空间，但是双向链表可以双向遍历，灵活性更高。
2）双向链表

struct DNode
{
    int value;       /* Data field */
    struct DNode *prior;  /* Pointer field */
    struct DNode *next;   /* Pointer field */
}DNode;
1
2
3
4
5
6

一、单向链表的ADT定义

1.1 创建链表
使用尾插法创建单链表

 //尾插法创建单链表、链表长度为n;
void CreatLinkedList(LinkedList &L,int n)  
{
    L = (LinkedList)malloc(sizeof(LNode));  //初始化;
    L->next = NULL;
    L->data = 0;
    LinkedList Tail = L;    //尾指针;
    cout<<"Enter "<<n<<" number(s)"<<endl;
    for(int i = 0 ; i < n; i++)
    {
        LinkedList Temp = (LinkedList)malloc(sizeof(LNode));
        cin>>Temp->data;
        Tail->next = Temp;
        Tail = Temp;
        Temp = NULL;
        L->data++;  //计数;
    }
    Tail->next = NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

1.2 查找
从头结点开始，逐个查找（后移）并计数，直到第i个为止。
算法的平均时间复杂度为T(n) = O(n)

//查找链表中第一个数据为data的节点，如果找到就返回节点指针，否则返回空指针NULL
Node findInList(LinkedList lst, int data) {
    Node tmp = lst;
    while (tmp->next != NULL) {
        if (tmp->data == data) {
            return tmp;
        }
        tmp = tmp->next;
    }
    return NULL;
}
1
2
3
4
5
6
7
8
9
10
11

1.3 插入
在指定位置插入节点

	// 在链表最前面插入一个节点，插入完成后，新插入的节点为链表的新的头结点
    void addHead(LinkedList* head, int val) {
        LinkedList* newNode = new Node();
        newNode->value = val;
        newNode->next = head->next;
    }

    // 在链表最后面添加一个节点
    void addTail(LinkedList* head, int val) {
        LinkedList* newNode = new Node();
        newNode->value = val;
        newNode->next = nullptr;
        LinkedList* cur = head;
        while(cur->next != nullptr){
            cur = cur->next;
        }
        cur->next = newNode;
    }

    // 在链表的某个位置插入一个节点
    void addIndex(LinkedList* head, int index, int val) {
        LinkedNode* newNode = new Node();
        LinkedNode* cur = _dummyHead;
        while(index--) {
            cur = cur->next;
        }
        newNode->next = cur->next;
        cur->next = newNode;
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

1.4 删除
删除结点

LinkedList* removeElements(LinkedList* head, int val) {
        //删除头节点
        while((head != NULL)&&(head->value == val)){ 
            Node* temp = head;
            head = head->next;
            delete temp;
        }
        //删除非头节点
        Node*  cur = head;  //头节点不动
        //不是空链表且不是尾部节点
        while((cur != NULL)&&(cur->next != NULL)){
        	//如果下一个节点的值等于目标值，删除
            if(cur->next->val == val){ 
                Node*  temp = cur->next; //
                cur->next = cur->next->next;
                delete temp; 
            }
            else{
                cur = cur->next;
            }
        }
        return head;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

1.5 反转链表

    Node* reverseList(ListNode* head) {
    	//初始化一个空指针的节点
        Node* pre = new Node();  
        pre = nullptr;
        ListNode* cur = new Node();
        cur = head;
        Node* temp;
        while(cur != nullptr){
            temp = cur->next; 
            cur->next = pre;
            pre = cur;
            cur = temp;
        }
        return pre;
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

1.6 链表的合并

有序表的合并，用链表实现：

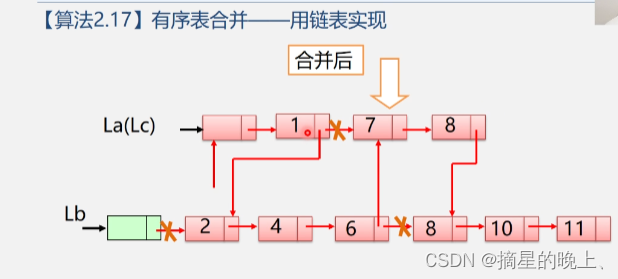
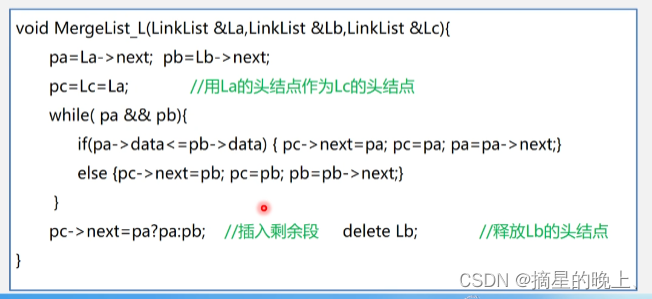
Node* mergeList(Node* head1, Node* head2)
	Node* p = head1; // 指向第一个链表的指针
	Node* q = head2; // 指向第二个链表的指针
	Node* dummy = new Node(); // 创建一个虚拟节点
	Node* r = dummy; // 指向新链表的指针
	while (p != nullptr && q != nullptr) {
	    if (p->val < q->val) {
	        r->next = p; // 将第一个链表中的节点插入到新链表中
	        p = p->next; // 移动指针到下一个节点
	    } else {
	        r->next = q; // 将第二个链表中的节点插入到新链表中
	        q = q->next; // 移动指针到下一个节点
	    }
	    r = r->next; // 移动指针到新链表的最后一个节点
	}
	if (p != nullptr) {
	    r->next = p; // 将第一个链表中剩余的节点插入到新链表中
	} else {
	    r->next = q; // 将第二个链表中剩余的节点插入到新链表中
	}
	head = dummy->next; // 将新链表头指针指向第一个节点
	return head;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

1.7 链表的长度

int getListSize(LinkedList* head){
	Node* p = head; // 指向链表头节点的指针
	int len = 0; // 链表长度
	while (p != nullptr) {
	    len++;
	    p = p->next; // 移动指针到下一个节点
	}
	cout << "链表的长度为：" << len << endl;
	return len;
}
1
2
3
4
5
6
7
8
9
10

二、链表的优缺点

链表的优点：
1）进行插入和删除元素的操作不需要移动其余元素，效率高，复杂度为O(1)；
2）链表不要求连续空间，空间利用效率高
链表的缺点：
1）查找元素和搜索元素的效率低，最快情况为O(1)，平均情况为O(N)

因此对于经常插入和删除的操作，数据结构采用 链表或者使用二叉搜索树。

参考资料：数据结构与算法基础课程-王卓老师