MixMatch: A Holistic Approach to Semi-Supervised Learning学习笔记

相关介绍

半监督学习已被证明是一种强大的学习范式，可以利用未标记数据来减轻对大型标记数据集的依赖。在这项工作中，本论文统一了目前半监督学习的主要方法，以产生一个新的算法，MixMatch，该算法为数据增强后产生的无标签示例猜测低熵标签，并使用MixUp混合有标签和无标签数据。MixMatch通过大量的数据集和标记数据量获得最先进的结果。

Q：什么是低熵标签？
A：低熵标签指的是远离决策边界。远离决策边界的数据密度会提升，数据出现的可能性会提升，信息熵就会下降。所以，低熵标签确保标签远离决策边界以提高其置信度。

主要思想

最近的许多半监督学习方法，通过在无标签数据上加一个损失项来使模型具有更好的泛化能力。损失项通常包含以下三种：

1. 熵最小化（entropy minimization): 鼓励模型在无标签数据上输出高置信度的预测结果
2. 一致性约束(consistency regularization): 鼓励模型在数据有扰动之后输出相同的概率分布
3. 通用正则化(generic regularization): 鼓励更好泛化和降低过拟合。

MixMatch通过将现有方法融合到一个损失里面，取得了很好的效果。

过程

给定一批具有one-hot标签的数据X和一批同样大小但是无标签的数据U，MixMatch产生一批数据增强后的带标签的数据X′ 和一批增强(对于每个无标签的数据进行K次随机增强)之后无标签的数据和它们猜测的标签(软标签)的U′。之后两个数据集被用来计算标记数据Loss和未标记的Loss。

损失函数

X ′ , U ′ = MixMatch ⁡ ( X , U , T , K , α ) L X = 1 ∣ X ′ ∣ ∑ x , p ∈ X ′ H ( p , p ⁡ model  ( y ∣ x ; θ ) ) L U = 1 L ∣ U ′ ∣ ∑ u , q ∈ U ′ ∥ q − p ⁡ model  ( y ∣ u ; θ ) ∥ 2 2 L = L X + λ U L U

$$\begin{aligned} \mathcal{X}^{\prime}, \mathcal{U}^{\prime} & =\operatorname{MixMatch}(\mathcal{X}, \mathcal{U}, T, K, \alpha) \\ \mathcal{L}_{\mathcal{X}} & =\frac{1}{\left|\mathcal{X}^{\prime}\right|} \sum_{x, p \in \mathcal{X}^{\prime}} \mathrm{H}\left(p, \operatorname{p}_{\text {model }}(y \mid x ; \theta)\right) \\ \mathcal{L}_{\mathcal{U}} & =\frac{1}{L\left|\mathcal{U}^{\prime}\right|} \sum_{u, q \in \mathcal{U}^{\prime}}\left\|q-\operatorname{p}_{\text {model }}(y \mid u ; \theta)\right\|_{2}^{2} \\ \mathcal{L} & =\mathcal{L}_{\mathcal{X}}+\lambda_{\mathcal{U}} \mathcal{L}_{\mathcal{U}} \end{aligned}$$ X′,U′LX​LU​L​=MixMatch(X,U,T,K,α)=∣X′∣1​x,p∈X′∑​H(p,pmodel ​(y∣x;θ))=L∣U′∣1​u,q∈U′∑​∥q−pmodel ​(y∣u;θ)∥22​=LX​+λU​LU​​
其中|X′|==Batch Size，|U′|==K倍的Batch Size，L是分类的个数，H(.)是简化的交叉熵函数。x，p分别是增强的有标签数据输入和标签，u,q是增强的无标签数据输入和标签。
X′ 和 U′ 分别对应着加强之后有本来就有标签和本来无标签的数据集，第一个Lx计算有标签的数据的交叉熵损失，第二个Lu(使用L2 Loss)是计算无标签数据的损失。

数据增强

对于没有标签的数据，进行K次增强，得到K个软标签(不是one-hot哪种标签，而是对于每个类别的概率),对 K 个结果求平均，这里的结果表示预测标签,使用sharpen算法对得到的预测标签的结果进行后处理，所谓sharpen，表示为:
$\mathrm{Sharpen}(p,T{)}_i:=p_i^{\frac{1}{T}}/{\sum }_{j=1}^L{p}_j^{\frac{1}{T}}$
整体流程如下图所示:

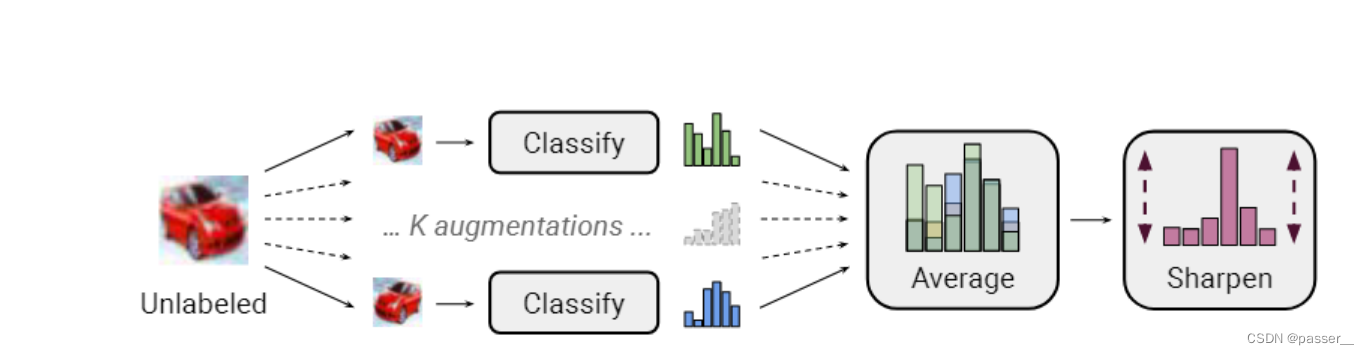
MixUp算法

本文所用的Mixup算法和Mixup论文提到的算法有一点点区别。基本流程如下:
λ ∼ Beta ⁡ ( α , α ) λ ′ = max ⁡ ( λ , 1 − λ ) x ′ = λ ′ x 1 + ( 1 − λ ′ ) x 2 p ′ = λ ′ p 1 + ( 1 − λ ′ ) p 2

$$\begin{array}{l} \lambda \sim \operatorname{Beta}(\alpha, \alpha) \\ \lambda^{\prime}=\max (\lambda, 1-\lambda) \\ x^{\prime}=\lambda^{\prime} x_{1}+\left(1-\lambda^{\prime}\right) x_{2} \\ p^{\prime}=\lambda^{\prime} p_{1}+\left(1-\lambda^{\prime}\right) p_{2} \end{array}$$ λ∼Beta(α,α)λ′=max(λ,1−λ)x′=λ′x1​+(1−λ′)x2​p′=λ′p1​+(1−λ′)p2​​
权重因子$\lambda$是使用超参数$\alpha$通过$Beta$函数抽样得到。通过这个流程可以看出来最后的x′更加和x1接近，p′同理。（原论文中没有max这一环节）

算法流程

3：对于带标签数据，对batch中每一个数据，做一次数据增强。
4&&5：对于无标签数据，对batch中每一个数据，做 K 次数据增强。
7：使用模型对无标签数据增强后的结果进行分类，对 K 个结果求平均，这里的结果表示预测标签。
8：使用sharpen算法对【7】的结果进行后处理
10：增强后的带标签数据重新组成一个batch
11：增强后的无标签数据和其通过【8】得到的预测标签组成 K 个batch
12：对【10】和【11】得到的数据进行concatenate和shuffle操作
13：对【10】得到的数据（一个batch大小）和【12】得到的数据的前一个batch大小的个数据，进行mixup操作，得到输出
14，对【11】得到的数据（ K个batch的大小 和【12】得到的数据的后 KB个数据（K个batch），进行mixup操作，得到输出

得到X′ 和 U′，对于X′ 数据计算标签和模型预测之间的交叉熵损失，对于U′ 计算 原来猜测标签和模型预测之间的L2损失(使用L2损失是因为它对于预测不正确不敏感），而且猜测标签的计算不回传梯度。

实验

实验好久完了

参考资料

https://zhuanlan.zhihu.com/p/529595891
https://zhuanlan.zhihu.com/p/66281890